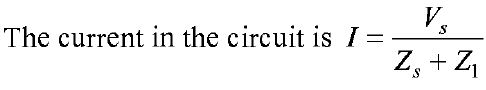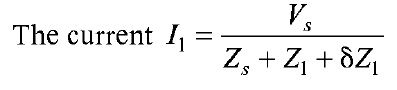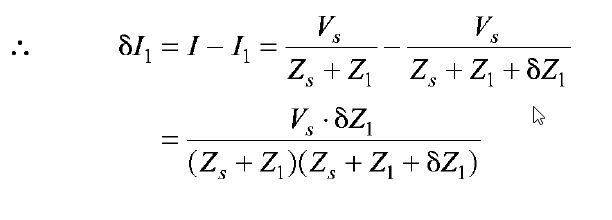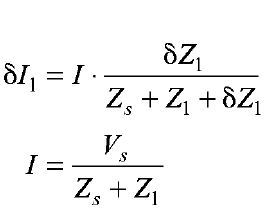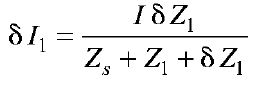Electrical Engineering ⇒ Topic : Compensation Theorem with sinusoidal excitation

Compensation Theorem

Compensation Theorem

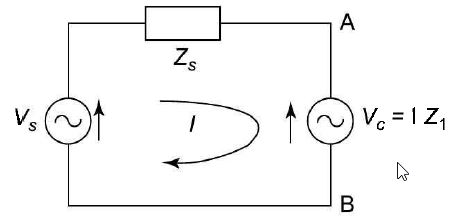
The compensation theorem states that any impedance having voltage across its terminal in the linear, bilateral network, may be replaced by a voltage source of zero internal impedance equal to the current passing through the impedance multiplied by the value of the impedance, provided the currents and voltages in other part of the network remain unaltered.

Let a branch of a network contain impedance Z₁ and Z₂. If the current in this branch is I, the voltage drop across Z₁ is IZ₁ with polarity as shown in Fig. 1 (a). Fig. 8.80(b) shows the compensation source Vc = IZ₁ which replace Z₁. However V_c must have polarity as shown in Fig. 8.80(b). If any chance which should effect /occurs in the network then the compensation source must be changed accordingly. The compensation is often referred as substitution theorem. This theorem is of use, when it is required to evaluate the changes in magnitudes of currents and voltages in the different branches of a network, due to a small change in the impedance of one of the branches

                                                  (a)                                                                                (b)                                  

                                                                                FIGURE (1)

Consider a network shown in Fig. 1 (a).

Let the impedance of branch AB change from Z₁ to (Z₁ + δZ₁). Let I₁ be the new current.

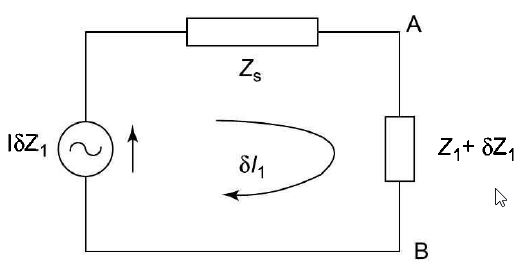
The impedance Z₁ of the network shown in Fig. 1 (a) may be replaced by a voltage source, V_C By substitution theorem V_c = IZ₁ with polarity as shown in Fig. 1 (c).

Similarly, the network shown in

Fig. 1 (b) can be replaced by the network shown in Fig. 1(d).

Let δI₁ denote the small change in current, due to the small change in the impedance value by δZ₁.

                                                        figure (d)

                                                        figure (e)

The network for which the above relationship holds good is as shown in Fig. 1 (e).

By compensation theorem the small change in the magnitude of current due to a small change in a branch  impedance is given by

Therefore, the original voltage source should be set equal to zero and a new voltage source IδZ₁ must be introduced with correct Fig.(e) polarity