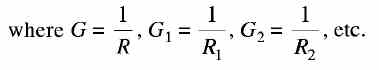Electrical Engineering ⇒ Topic : Parallel Circuits
|
|
| William
| |
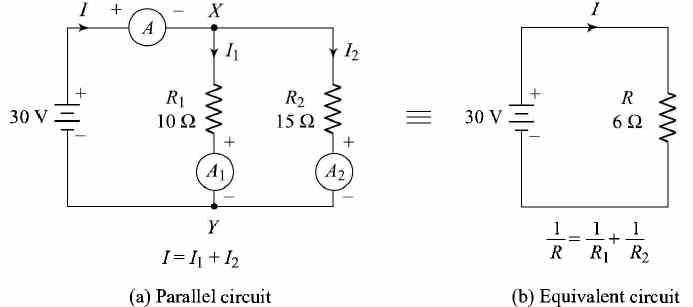
Parallel Circuits In parallel circuits, each resistance (load) is connected directly across the voltage source, as shown in Fig. (1). Thus, there are many separate paths for current flow. The voltage across all parallel branches is the same. Therefore, the current -in each branch is different and depends only on the resistance in the branch . FIGURE (1) Resistances connected in parallel In Fig. 1 (a) two resistances R1 and R2 are connected in parallel. The currents through R1 and R2 are measured by ammeters A1 and A2. The total circuit current (I) is read by ammeter A. The voltage across the circuit (V) is read by voltmeter V. Applying Ohm's law, /1 = V/R1 and I2 = V/R2. If lis the total current in the circuit, then If R in Fig. 1 (b) represents the resistance of a single or equivalent resistor across which is applied the voltage V, and if V produces a current I through resistance R, then Equations (1) and (2) represent the same current I, and therefore equating these two equations, we get If the circuit consists of more than two resistors in parallel, the equivalent resistance can be expressed as By applying this expression to the values given in Fig. 1 (a), we get Reciprocal of the resistance, that is, 1/R is called conductance. The symbol commonly used for conductance is G and the unit of conductance is 'Siemens'. From Eq. (4) it follows for parallel circuits that G= G1+ G2 + G3 ... + Gn ................... (5)
| |
|
| |
!! OOPS Login [Click here] is required for more results / answer

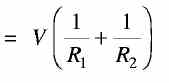 ................ (1)
................ (1)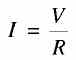 ............... (2)
............... (2)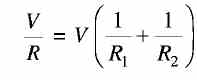
 .................. (3)
.................. (3)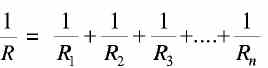 ............. (4)
............. (4)