Electrical Engineering ⇒ Topic : Reciprocity Theorem
|
|
| Samual
| |
RECIPROCITY THEOREM This theorem states that In any linear bilateral network, the current (I) through any branch of the network due to a single voltage source V elsewhere in the network is equal to the current through the branch of the network where the source was originally placed if the source is placed in the branch in which the current (I) was originally determined. Explanation In Figure 1 (a), the source is shown and the current through the resistor r4 is I1. In Figure 1 (b), the source is placed in series with r4 and the current through r1 is I2 By Reciprocity theorem I1 = I2 (A) (B) FIGURE The main limitation of this theorem is that it is applicable only to single source networks and not to a multi-source network. Another point is that the network should not have any time varying element | |
|
| |
| Mason
| |
This theorem permits us to transfer voltage/current source from one position in the circuit to another and is applicable to circuits which contain only one voltage source or one cun-ent source. It may be stated as under. In any linear bilateral circuit, if a voltage source acting in branch X causes a current I in branch Y, then shifting the voltage source (but not its impedance) to branch Y will cause the same current I in branch X However, currents in the other parts of the circuit will not remain the same after this interchange. The dual is also true : If current applied at node A of the circuit produces voltage V at another node B, then the same cun-ent applied at node B will produce the same voltage V at node A. The reciprocity theorem seems quite strange but it is true | |
|
| |
| William
| |
Reciprocity Theorem Reciprocity theorem can be stated as follows: "If in any network, a potential V introduced into any branch A causes a current I to flow in any other branch B; then the same potential V introduced into branch B will cause the same value of current to flow in branch A". In other words, this law simply means that V and I are mutually interchangeable. The ratio V/I called the transfer resistance (or impedance). For example,consider the network shown in Fig.(1). Applying Kirchhoff's second law to Fig. (1) (a), we get V = I1R1+ (I1 - I2) R3 = I1 (R1 + R3) - I2R3 ...........(1) Also, 0 = I2R2 - (I1 - I2) R3
Similarly, applying Kirchhoff's second law to Fig. 1 (b), we get V = I1' R2 + (I'1 - I'2) R3 = I1' (R2 + R3) - I'2 R3 ..................... (2) 0 = I2'R1 - (I'1 - I'2) R3
Substituting for I'1 in Eq. (2), we get From the above, it can be seen that I2 = I'2. The ratio V/I2 is called the transfer resistance and is given by
In case of ac circuits, the transfer impedance = (Z1 + Z2) + (Z1 Z2/Z3)
| |
|
| |
!! OOPS Login [Click here] is required for more results / answer
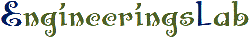

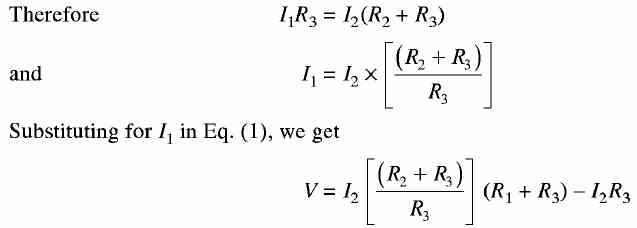
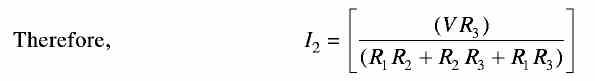 .............. (a1)
.............. (a1)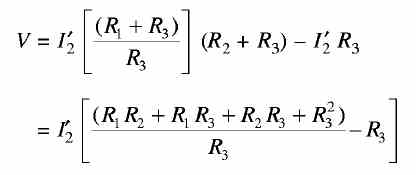
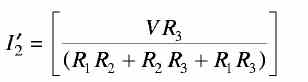 ...................(a2)
...................(a2)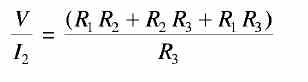
 ........... (3)
........... (3)