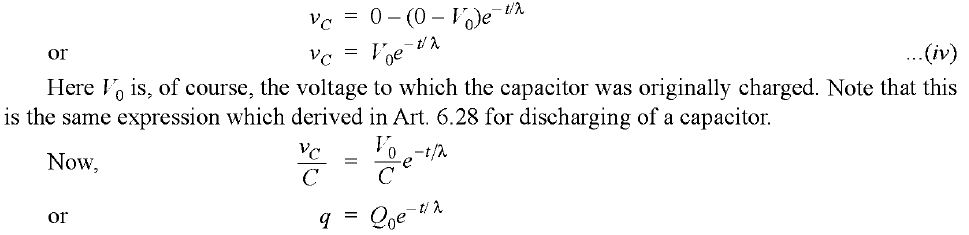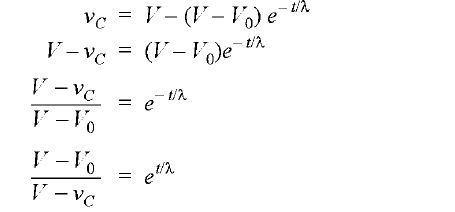Electrical Engineering ⇒ Topic : Transient Relations During Charging/Discharging of Capacitor
|
|
| Peter
| |
Transient Relations During Charging/Discharging of Capacitor When a capacitor is charging or discharging, it goes from one steady-state condition (called initial condition) to another steady-state condition (called final condition). During this change, the voltage across and current through the capacitor change continuously. These are called *transient conditions and exist for a short duration. It can be shown mathematically that voltage vc, across the capacitor at any time t during charging or discharging is given by
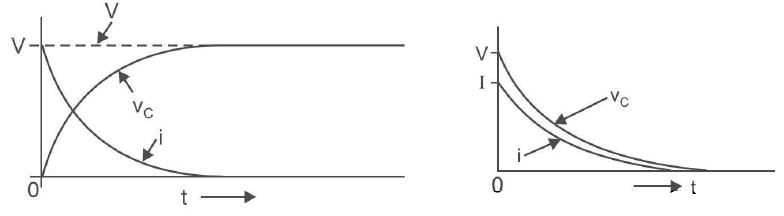
1. Transient conditions during charging. When we charge an uncharged capacitor, VO = 0 so that eq. (i) becomes This is the same equation that we derived in Art for charging of a capacitor . Note that eq. (iii) is the same that we derived in Art for charging of a capacitor. Fig.(a) shows capacitor voltage (vc) and charging current (i) waveforms for a charging capacitor. It may be seen that voltage across the capacitor is building up at an exponential rate while the charging current is decreasing at an exponential rate. (a) (b) figure (2). Transient conditions during discharging. For discharging of a capacitor, V = 0 because there is no source voltage. Therefore, eq. (i) becomes
where Q0 is the initial charge on the capacitor and q is the charge on the capacitor at time t. Similarly, i = I0e-t/λ where I is the initial discharging current and i is the discharging current at time t. Fig. (b) shows the capacitor voltage and discharging current wave forms. Both decrease at exponential rate and reach zero value at the same time. Time for charge or discharge. Sometimes it is desirable to determine how long will it take the capacitor in RC series circuit to charge or discharge to a specified voltage. This can be found as follows : From eq. (i) Taking the natural log, we have,
| |
|
| |
!! OOPS Login [Click here] is required for more results / answer
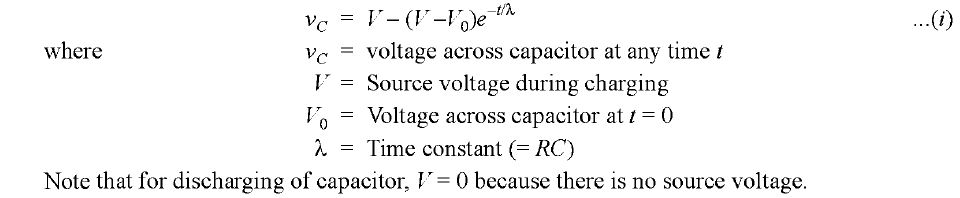
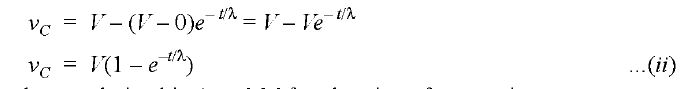
 \
\