Electrical Engineering ⇒ Topic : Current and kVA at Maximum Efficiency

Let us assume the iron losses = P_i

The total copper losses referred to the primary side =

From Equation ,

                                          ........... (1)

In a given transformer, V₁ is approximately constant and hence for a given value of /₁ and cos Φ₁ the efficiency will be maximum when the denominator of Eq. (1) is minimum. Thus, differentiating both the sides with respect to /₁, we get

will be maximum when d/d/₁ = O

                                                                  ...........  (2)

Hence, the efficiency of a transformer is maximum when the variable copper loss is equal to the constant iron loss. From Eq. (2), it follows that at maximum efficiency, the primary current

Similarly, at maximum efficiency, the load current

                                                                            .............. (3)

where R_e2 is the equivalent resistance of the transformer referred to the secondary side given by R_e2 = R₂ + (V₂/V₁)²R₁  The efficiency versus load current curves are shown in Figure for different power factors

             FIGURE  (a) Efficiency of a transformer as a function of the load current for different power factors

For a given transformer, the efficiency decreases with a decrease in power factor. Distribution transformers are generally designed to give maximum efficiency at 75% of full-load

CURRENT AND kVA AT MAXIMUM EFFICIENCY

Let

S_fl = V₂I₂ is full load in V_A, S_m = V₂I_m in VA at maximum efficiency, I_2m secondary current at maximum efficiency, I_2fI is full-load secondary current, and P_cufl cup is copper loss at full load

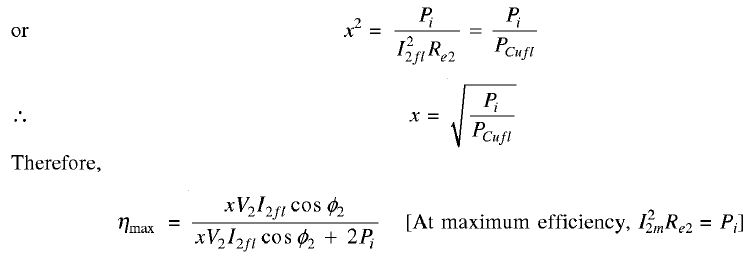
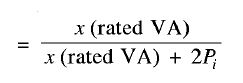                                                   ............. (1)