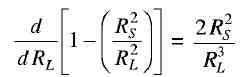Electrical Engineering ⇒ Topic : Maximum Power Transfer Theorem
|
|
| Samual
| |
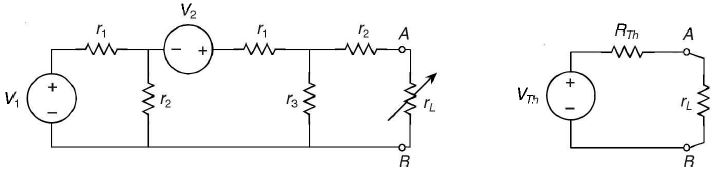
MAXIMUM POWER TRANSFER THEOREM This theorem is useful to determine the value of load resistance for which there would be maximum amount of power transfer from source to load. This theorem states that a resistive load connected to a DC network receives maximum power when the load resistance is equal to the internal resistance of the source network as seen from load terminals Explanation In Figure 1 (a), the load resistance is connected across the terminals A-B. By applying Thevenin's theorem, its equivalent Thevenin's circuit of the DC network across A-B is depicted in Figure 1 (b).
(a) (b) figure (1) With reference to Figure 1(b), the current through the load resistance rL is given by The power delivered to the resistive load is given by Now, by adjusting the value of rL, the maximum power can be delivered through rL if and only if (dPL/drL) = O. It is clear that the maximum power is transferred to load resistance if the load resistance is equal to the internal resistance of the source network | |
|
| |
| Leo
| |
This theorem deals with transfer of maximum power from a source to load and may be stated as under : In d.c. circuits, maximum power is transferred from a source to load when the load resistances made equal to the internal resistance of the source as viewed from the load terminals with load removed and all e.m.f sources replaced by their internal resistances
FIGURE (A) Figure (i) shows a circuit supplying power to a load RL. The circuit enclosed in the box can be replaced by Thevenin's equivalent circuit consisting of Thevenin voltage V = VTH in series with Thevenin resistance R,(=RTH) as shown in Figure A (ii). Clearly, resistance R. the resistance measured between terminals AB with RL removed and e.m.f. sources replaced by their internal resistances. According to maximum power transfer theorem, maximum power will be transferred from the circuit to the load when RL is made equal to RP, the Thevenin resistance at terminals AB. | |
|
| |
| William
| |
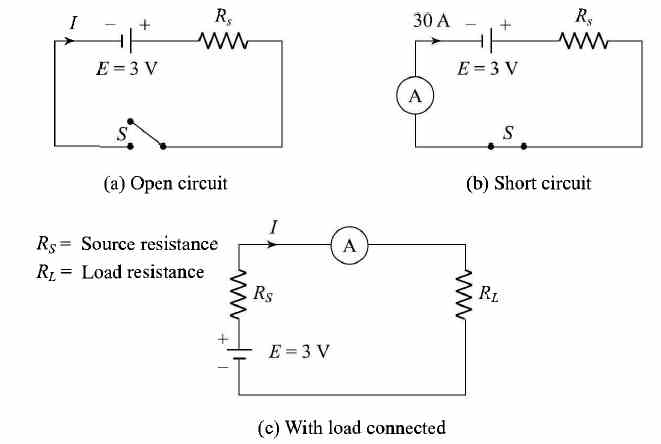
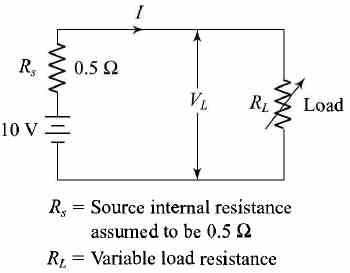
Maximum Power Transfer Theorem This has already been discussed in Sec. 3.6.1 and Figs. (1) and (2). As already shown in the above section, the maximum power transferred to the load = I2 RL where, RL is the load resistance as shown in Fig. (2) If Rs is the internal resistance of the source of emf, then the current through the circuit is
Figure (1) Effect of source resistance on load current, voltage and maximum power transfer
Figure (2) Circuit to demonstrate the effect of source resistance on the power transferred to the load
This power is maximum when the denominator of the above equation is minimum i.e. when RL = RS .................... (3) To check that the above condition gives the minimum value of the denominator in Eq. (2), the Eq. (3) should be differentiated with respect to RL. This gives This quantity is always positive and therefore RL = Rs is the condition when the denominator of the Eq. (1) is minimum and therefore the output power is maximum. Thus, the power transferred from the source to the load is maximumwhen the resistance of the load is equal to the internal resistance of the source.This condition is called "resistance matching". Resistance matching is of practical importance in electronic and communication circuits when the source resistance is very high and when it is necessary to transfer the maximum possible amount of power from the source to the load. In the case of dc generators and secondary batteries, the internal resistance is normally low and the above condition carmot be easily satisfied without overloading the source. | |
|
| |
!! OOPS Login [Click here] is required for more results / answer
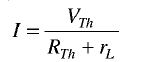 ............ (1)
............ (1)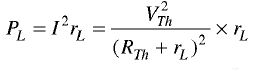 ............. (2)
............. (2)

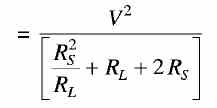 .............(1)
.............(1)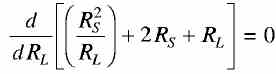
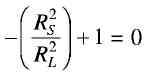 ............ (2)
............ (2)