Electrical Engineering ⇒ Topic : Magnetic Field Intensity (H) due to a Thin Straight Line of Current of Infinite Length
|
|
| Peter
| |
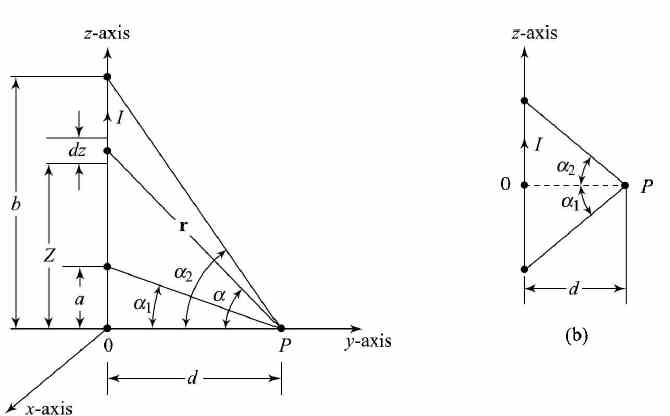
Magnetic Field Intensity (H) due to a Thin Straight Line of Current of Infinite Length Although all current carrying conductors occupy finite area of cross-section, in many cases they are of such small dimensions that the magnetic effects at distances fairly away from them are essentially the same as though the current is passing through a thin line (wire). Further, the study of the magnetic effect of thin current carrying wires provides the basis for an understanding of the behaviour of current carrying systems with larger dimensions. Consider a finite thin current carrying conductor along the z-axis as shown in Fig. 1 (a). The conductor is placed at z = a and extends up to z = b. Let P be a point on the y-axis with coordinates (0, d, 0), where 0 is the origin of reference. Let I be the current through the conductor. Consider an element dz at a distance z from O. figure (1) Magnetic field due to a straight line (wire) of current The differential magnetic field intensity due to I dz at point P will act into the paper, and in cylindrical coordinates is given by dH= aΦ (I . dz x r / 4πr3) where aΦis the unit vector in the cylindrical coordinate system indicating the direction of dH (aΦ is normal to the plane of the paper at P and is directed into the paper).
where α1 and α2 are angles as shown in the figure. Also, α1 and α2 will be positive when a and b are positive. If the thin line (wire) extends to both sides of 0, then α1 becomes negative. The following cases can be visualised. Case (a) When P is midway between the line, i.e. b = -a, then α2 = -a1 as shown in Fig. 1 (b).
2 α is the angle subtended by the line (wire) at P. Case (b) If the thin line is of semi-infinite length, then α = π/2.
Case (c) If the thin line is semi infinite, then al = 0 and a2 = π/2. i.e. a = 0 and b tends to infinity. Then
From the above, it can be seen that the magnetic field intensity (H) due to a thin finitely long wire is H = (aΦI/2 πd) A/m from Eq. (3). And, the direction of H is into the paper at point P. The magnitude of H is directly proportional to the strength of the current and is inversely proportional to the distance of the point P from the wire | |
|
| |
!! OOPS Login [Click here] is required for more results / answer

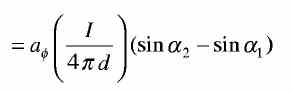 ..............(1)
..............(1)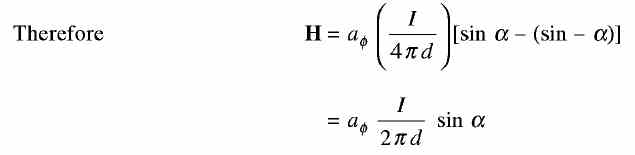 ................ (2)
................ (2) (From Eq. (2)) ............. (3)
(From Eq. (2)) ............. (3)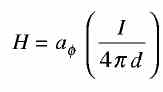 (from Eq. (1)) ................. (4)
(from Eq. (1)) ................. (4)