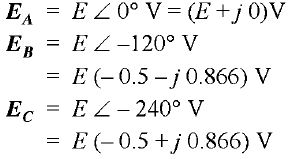Electrical Engineering ⇒ Topic : Elementary Three-Phase Alternator

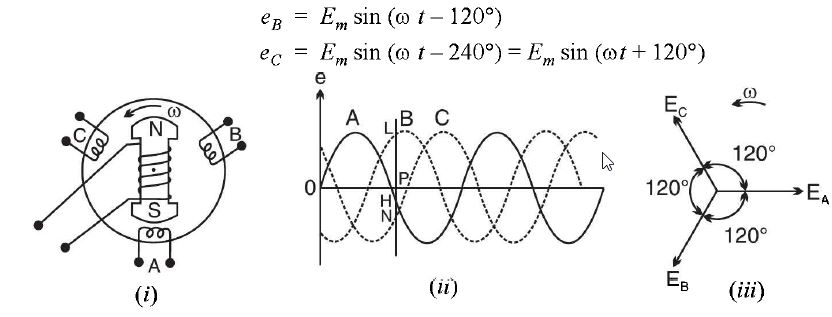
Elementary Three-Phase Alternator

In an actual 3-phase alternator, the three windings or coils are stationary and the field **rotates. Fig. a (i) shows an elementary 3-phase alternator. The three identical coils A, B and C are symmetrically placed in such a way that e.m.f.s induced in them are displaced 120 electrical degrees from one another. Since the coils are identical and are subjected to the same uniform rotating field, the e.m.f.s induced in them will be of the same magnitude and frequency. Fig. a (ii) shows the wave diagram of the three e.m.f.s whereas Fig.a (iii) shows the phasor diagram. Note that r.m.s. values have been used in drawing the phasor diagram. Thus E_A is the r.m.s. value of the e.m.f. induced in coil A. The equations of the three e.m.f.s are

                                                   e_A = E_m sin ω t

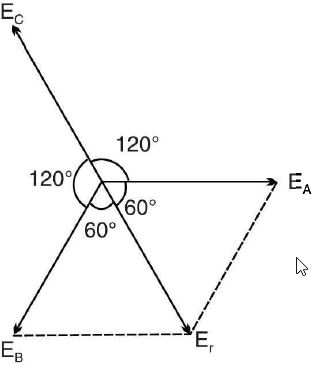
                                                                                   figure (a)

  It can be proved in many ways that the sum of the three e.m.f s at every instant is zero.

(i)                                                        Resultant = e_A+e_B+ e_c

(2) Referring to the wave diagram in Fig. a (ii), the sum of the three e.m.f.s at any instant is zero. For example, at the instant P, ordinate PL is positive while the ordinates PN and PH are negative. If you make actual measurements, it will be seen that

                                                            PL + (- PN)+ (- PH) = 0

(3) Since the three windings or coils are identical, E_A = E_B = E_C = E (in magnitude). As shown in Fig. B, the resultant of E_A and E_B is E_r and its magnitude is = 2E cos: 60° = E. This resultant is equal and opposite to E_c. 

Hence the resultant of the three e.m.f.s is zero.

(4) Using complex algebra, we can again prove that the sum of the three e.m.f.s is zero. Thus taking E_A as the reference phasor, we have,

                                                  figure (b)

E_A+ E_B+ E_C = (E +j0) + E (- 0.5 - j 0.866) +E (-0.5 + j 0.866) = 0

The reader may wonder how we can get power from the terminals of a 3-phase alternator if the sum of the voltages it delivers is zero at every instant ? This will be explained when we come to the connections of the three phases or windings.