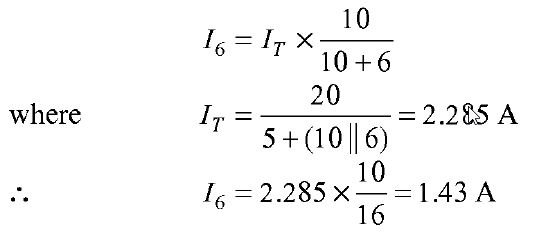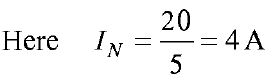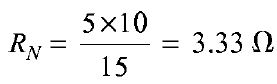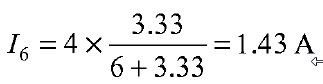Electrical Engineering ⇒ Topic : Nortons Theorem with d.c

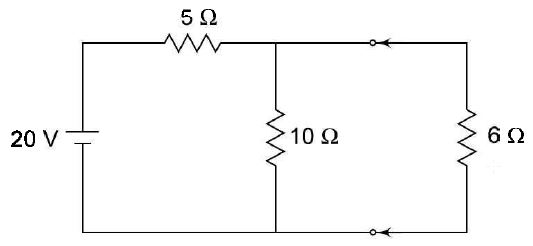
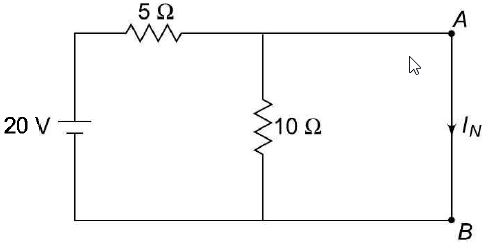
Norton's Theorem with d.c

Another method of analysing the circuit is given by Norton's theorem, which states that any two terminal linear network with current sources, voltage sources and resistances can be replaced by an equivalent circuit consisting of a current source in parallel with a resistance. The value of the current source is the short circuit current between the two terminals of the network and the resistance is the equivalent resistance measured between the terminals of the network  with all the energy sources are replaced by their internal resistance.

   According to Norton's theorem,an equivalent circuit can be found to replace the circuit in Fig. (a).

In the circuit if the load resistance 6Ω  is connected to Norton's equivalent circuit, it will have the same current through it and the same voltage across its terminals as it experiences in the original circuit. To verify this, let us find the current passing through the 6Ω  resistor due to the original circuit

                                                                               figure (a)

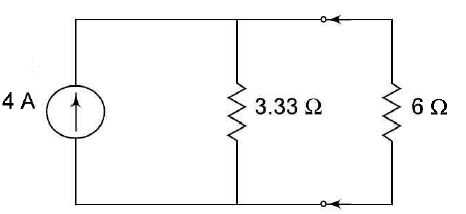
i.e. the voltage across the 6 Ω resistor is 8.58V. Now let us find Norton's equivalent circuit. The magnitude of the current in the Norton's equivalent circuit is equal to the current passing through short circuited terminals as shown in Fig. (b).

                                                                       figure (b)

Norton's resistance is equal to the parallel combination of both the 5 Ω and 10 Ω resistors

                                                                                       figure (c)

The Norton's equivalent source is shown in Fig. (c).

Now let us find the current passing through the 6 Ω, resistor and the voltage across it due to Norton's equivalent circuit.

The voltage across the 6 Ω, resistor = 1.43 X 6 = 8.58 V

Thus, it is proved that R_L (= 6 Ω) has the same values of current and voltage in both the original circuit and Norton's equivalent circuit